prgmTrouble wrote:
Gravity is directly proportional to distance and mass:
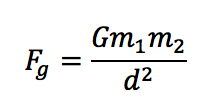
Just assume the spacecraft mass is one, and then you only have to mod the mass of the planet and the distance. G = 6.674×10^(−11) N · (m/kg)^2
Forces:
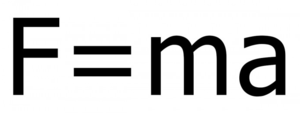
Since we are assuming mass of the spacecraft is one, we have a direct proportion which states force = acceleration. Then factor in a direction using trigonometry where needed and subtract all relevant force vectors (thrust, gravity, and air resistance) to get a net force. Then divide by one and you have acceleration.
Kinematics:
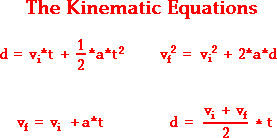
With acceleration already sorted out, anything else you need is found with the kinematic equations. Just remember that acceleration changes direction constantly if you move around the center rather than just away.
Hope this helps!
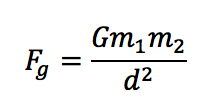
Just assume the spacecraft mass is one, and then you only have to mod the mass of the planet and the distance. G = 6.674×10^(−11) N · (m/kg)^2
Forces:
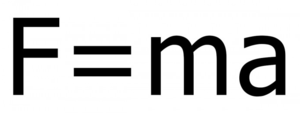
Since we are assuming mass of the spacecraft is one, we have a direct proportion which states force = acceleration. Then factor in a direction using trigonometry where needed and subtract all relevant force vectors (thrust, gravity, and air resistance) to get a net force. Then divide by one and you have acceleration.
Kinematics:
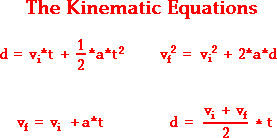
With acceleration already sorted out, anything else you need is found with the kinematic equations. Just remember that acceleration changes direction constantly if you move around the center rather than just away.
Hope this helps!
Just an idea, if you have more time and want to make the physics of the game more accurate (and more complex) you have to use the Tsiolkovsky rocket equation. F=ma assumes that mass is held constant; however, in a rocket mass is constantly decreasing because the burning propellant is constantly being expelled. The Tsiolkovsky rocket equation is as follows:
ΔV = Vex × ln (mi / mf)
ΔV: Change in velocity
Vex: Velocity of the Propellant
mi: initial mass (the rocket body + the total propellant)
mf: final mass (basically the rocket's mass after all the propellant has been burned and expelled)
The change in velocity is equal to the exhaust velocity of the propellant times the natural log of the inital mass divided by the final mass.
The equation can also be rearranged to give this:
mi/mf = exp(ΔV/Vex)
An example:
In order to keep an object in Low Earth Orbit(LEO) an object should be traveling at around 9000 m/s (this is the change in velocity or ΔV).
We assume our rocket is a chemical rocket that can expel its propellant at 4000 m/sec (this is the exhaust velocity or Vex).
Thus
mi/mf = exp(-9000 / 4000) =
mi/mf = exp(-2.25)=
mi/mf = 0.105 = 10.5%
The ratio between the initial mass and the final mass is 11%. This means that 89% of the rocket's inital mass has to be gone by the time all of the propellant is burned away. Basically 89% of the rocket's total mass has to be propellant and so only 11% can be devoted to the rocket body, payload, life support, etc. If you've ever wondered why its expensive to get a kilogram to orbit this is why.
Note: I am not a rocket scientist or engineer so I if there are real rocket scientists or engineers or more knowledgeable people here feel free to correct me.
Here's a basic aerospace engineering course if you want to learn more:
https://www.edx.org/course/introduction-aerospace-engineering-mitx-16-00x-0
Good Luck!



























