- [Matlab] Laplacian Circular Membrane Mode Simulator
- 27 Feb 2009 01:21:23 pm
- Last edited by KermMartian on 20 Nov 2016 02:34:36 pm; edited 2 times in total
On a whim, I wrote a program in matlab to simulate the modes of a 2D circular membrane vibrating in 3D space, also known as a drum. The program takes the two variables for the mode of the membrane (n,m), where n is the number of radial nodes, and m is the number of concentric nodes (1=none only center and edge, 2=center, edge, and 1 more, etc), then generates a plot of the membrane, using Laplacian smoothing to create the surface. However, it still has a significant number of flaws, so if anyone would like to mess with my code and see if they can improve it a bit, I'd appreciate the help. Check out some sample plots and the code itself below.
drumsolve(8,8);
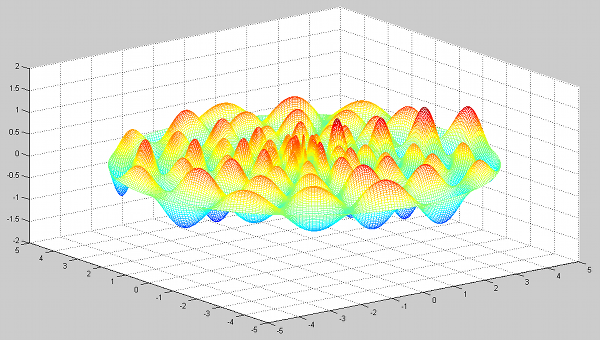
drumsolve(2,6);
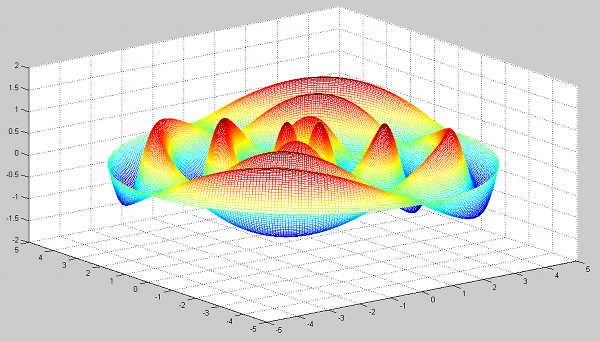
drumsolve(6,2);
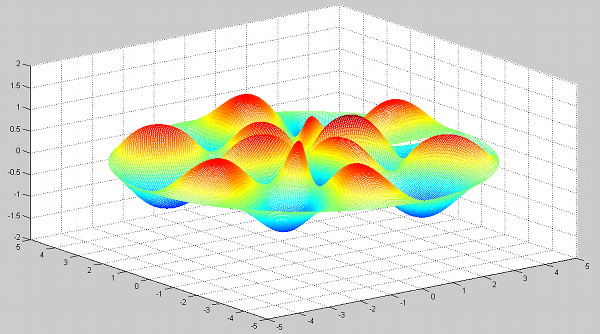
drumsolve(2,1);
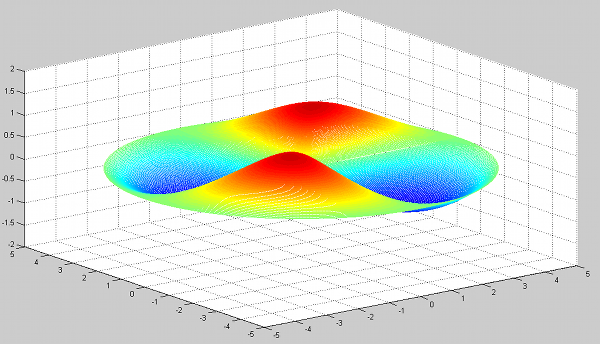
Code:
drumsolve(8,8);

drumsolve(2,6);

drumsolve(6,2);

drumsolve(2,1);

Code:
% Christopher Mitchell, www.cemetech.net
% Circular Membrane (Drum) Mode Solver/Simulator
function [] = drumsolve(n,m)
gran_rad=0.02;
gran_theta=(2*pi)/360;
changetol = 0.0001;
radmax = 5;
zmax = 1;
rad=[0:gran_rad:radmax];
theta=[0:gran_theta:2*pi];
%generate the polar mesh
for a=1:length(rad)
x(:,a)=rad(a)*cos(theta);
y(:,a)=rad(a)*sin(theta);
movable(1:length(theta),a)=1;
end
%set up immovable radii
if (n>0)
for a=1:n
myangle=(a-1)*(pi./n);
movable(1+round(myangle./gran_theta),:)=0;
z(1+round(myangle./gran_theta),:)=0;
movable(1+round((pi+myangle)./gran_theta),:)=0;
z(1+round((pi+myangle)./gran_theta),:)=0;
end
end
% set up immovable concentric circles
if (m>0)
for a=1:m+1
myrad=(a-1)*(radmax/m);
movable(:,1+round(myrad./gran_rad))=0;
z(:,1+round(myrad./gran_rad))=0;
end
end
%set up initial z values to smooth
rowstart = 1;
for b=2:length(rad)-1
if (m==0 || movable(2,b)==1)
blockstart = rowstart;
for a=1:length(theta)
if movable(a,b)==1
z(a,b)=blockstart;
else
blockstart=blockstart*-1;
end
end
else
rowstart = rowstart*-1;
end
end
%smooth it out using Laplace's method
done=0;
while done==0
done=1;
for b=1:length(rad)
for a=1:length(theta)
if (movable(a,b) == 1)
div = 3;
if (a==1)
neighbortotal = z(length(theta),b);
else
neighbortotal = z(a-1,b);
end
if (a==length(theta))
neighbortotal = neighbortotal+z(1,b);
else
neighbortotal = neighbortotal+z(a+1,b);
end
if (b>1)
neighbortotal = neighbortotal+z(a,b-1);
else
neighbortotal = neighbortotal+z(mod((a+round(pi./gran_theta)-1),length(theta))+1,2);
end
if (b<length(rad))
neighbortotal = neighbortotal+z(a,b+1);
div = div+1;
end
new = neighbortotal./div;
if abs(new-z(a,b))>changetol
done = 0;
end
z(a,b)=new;
end
end
end
end
z=z.*zmax./max(max(abs(z)));
figure(1);
for i=1:5;
for rho=0:pi./12:2*pi;
coeff = sin(rho);
clf;
mesh(x,y,coeff.*z);
axis([-radmax radmax -radmax radmax -2*zmax 2*zmax -1*zmax zmax]);
M(1)=getframe();
end
end











